Dijkstra's Algorithm - Shortest Path Finding

Dijkstra's Algorithm - is the one of the most classical algorithm for shortest path finding. If someone has to find the shortest path of a given problem, it's the way to go algorithm.

It's used to find shortest distance of nodes in a graph from the source node. That means it finds shortest distance for each node from the source node. 

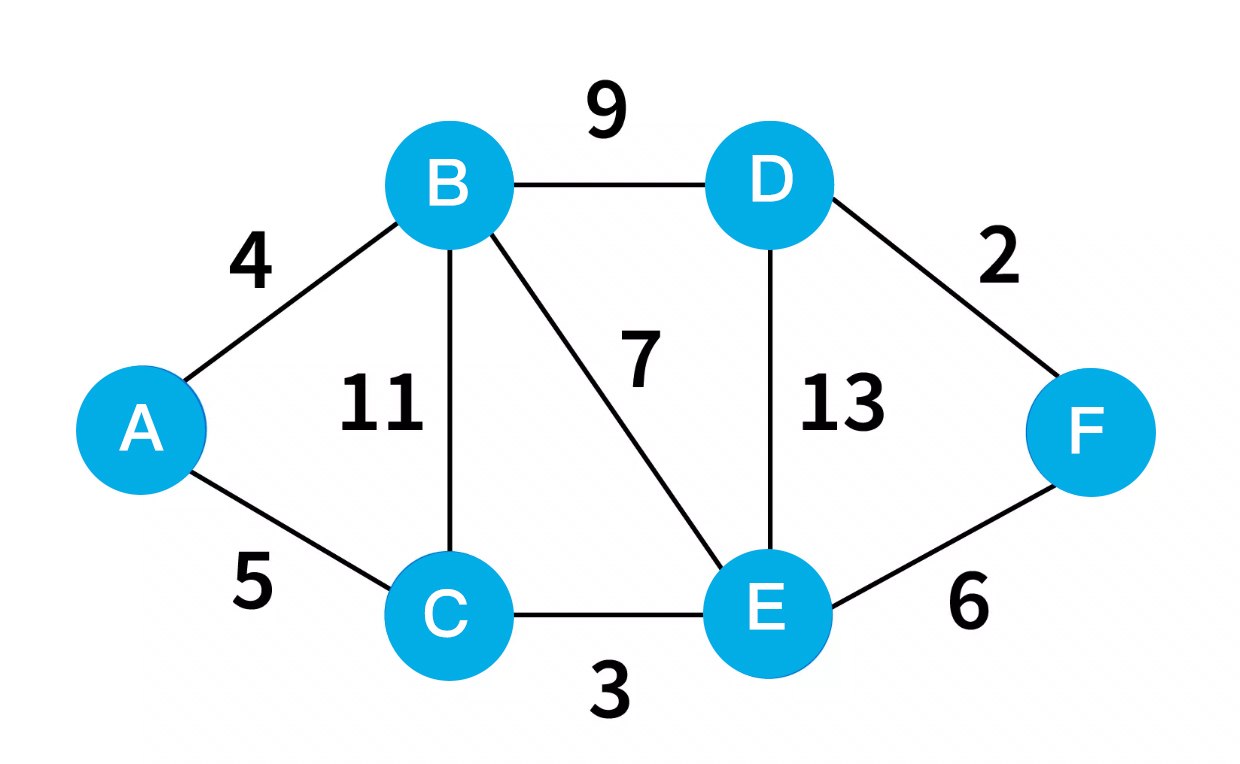
Here we will use the above graph to demonstrate Dijkstra-s Algorithm - Shortest Path Finding.

Here there are few terms used for the algorithm

1. visited
2. unvisited 
3. marked updated

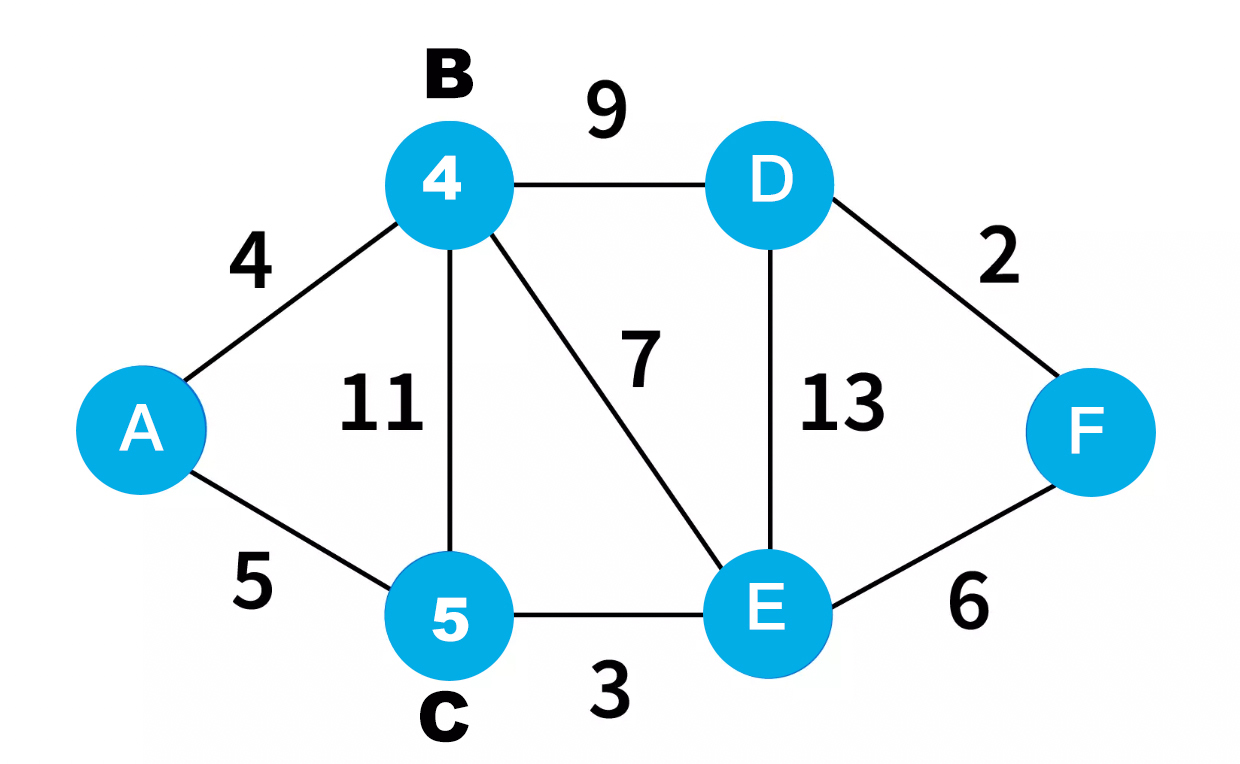
Initially everything is started unvisited and we can pick any node in the graph as source node. For convenience we will mark node A source and unvisited as well. Apart from source node other nodes values are marked as infinity.

Here if we visit from A to B we will be counting cost. Here you may also call it distance. So from A to B the cost or distance is 4. In this case, this is also the shortest distance.

Visit node C

Now visit node C becomes interesting. There are two ways to visit node C, we can directly visit node C from A, or first we can visit B and then go to C. Definitely we can see to node C, the shortest path is from A.

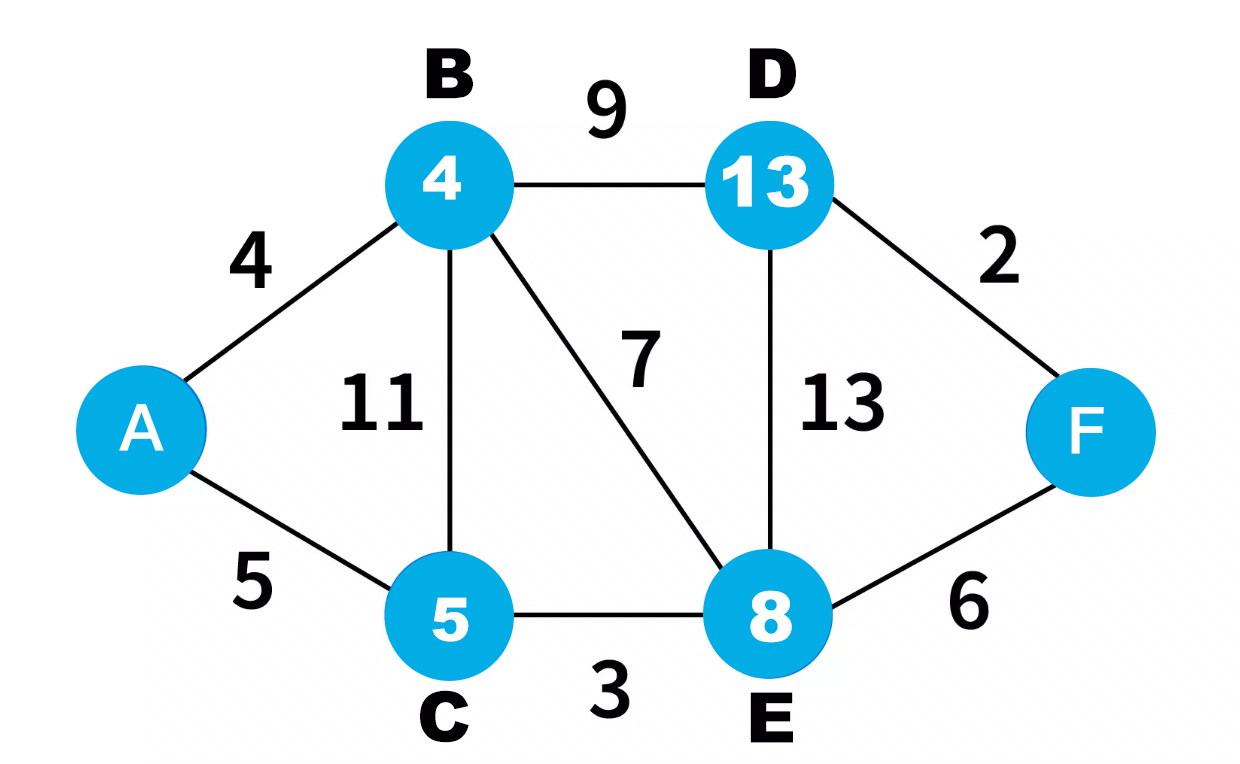
This is where Dijkstra-s Algorithm shines and finds the shortest path and update the value. This kind of updating shortest value to a node is called relaxation. Let's get started and find the shortest path for all the nodes.

Relaxation

Here we use a terminology called relaxation, we also say we relax nodes to go to other nodes to find the shortest path. For example, when we go to C node from A through B, we find a distance. So first we relax B and then relax C. But we can also go to C from A directly. So to C is the shortest path is from A. You can also say we have relaxed edge B.

Relaxation is trying different edges to find the shortest path.

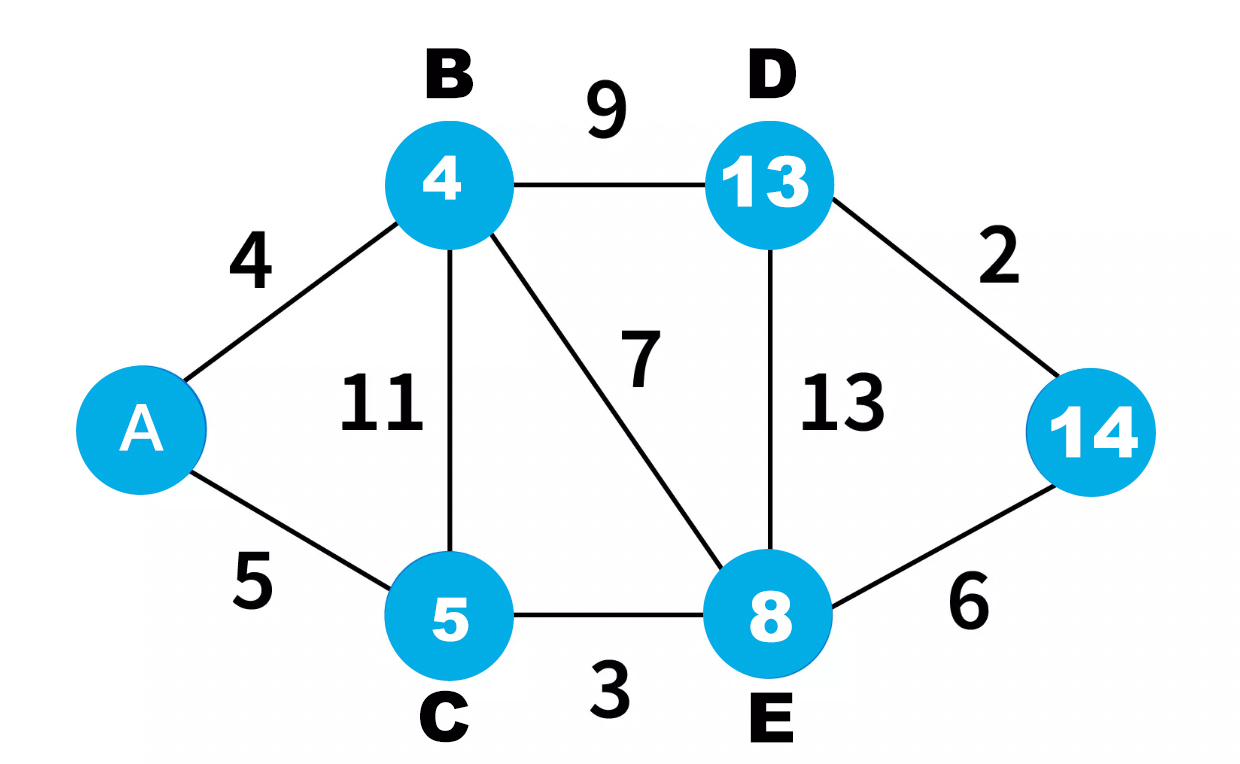
Let's find the shortest path

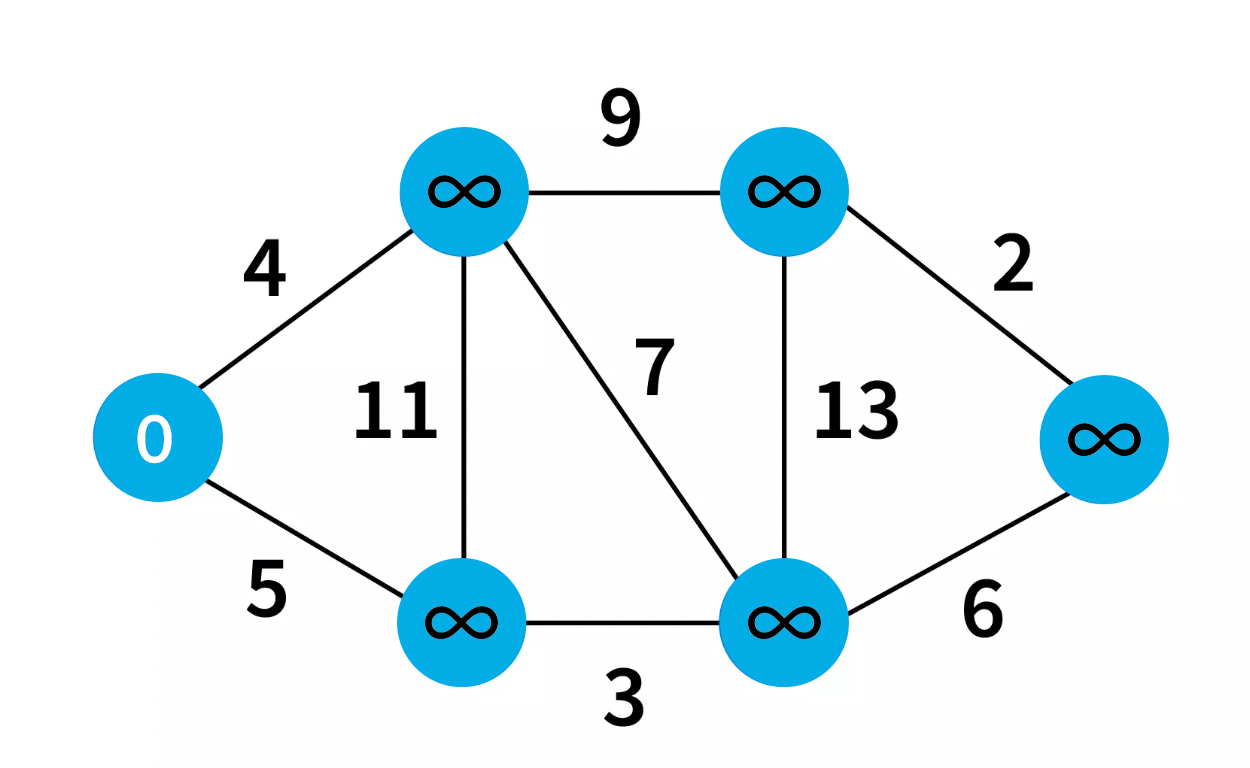
Initially all the vertices are set to infinity except from the source node. In our case this is the first one with value 0.

So initially from A to A path value is 0. So 0 is assigned at the A vertex. From A to B the path value is infinity but the edge value is 4. Do remember the edge value is always assigned randomly from the beginning.

Learn more about edge relaxation here

  if ( d[u] + c(u, v) < d[v] ) then
  {
    d[v] = d[u] + c(u, v)
  }

The above is the pseudo code for edge relaxation and updating path value. Here we will understand it by below example

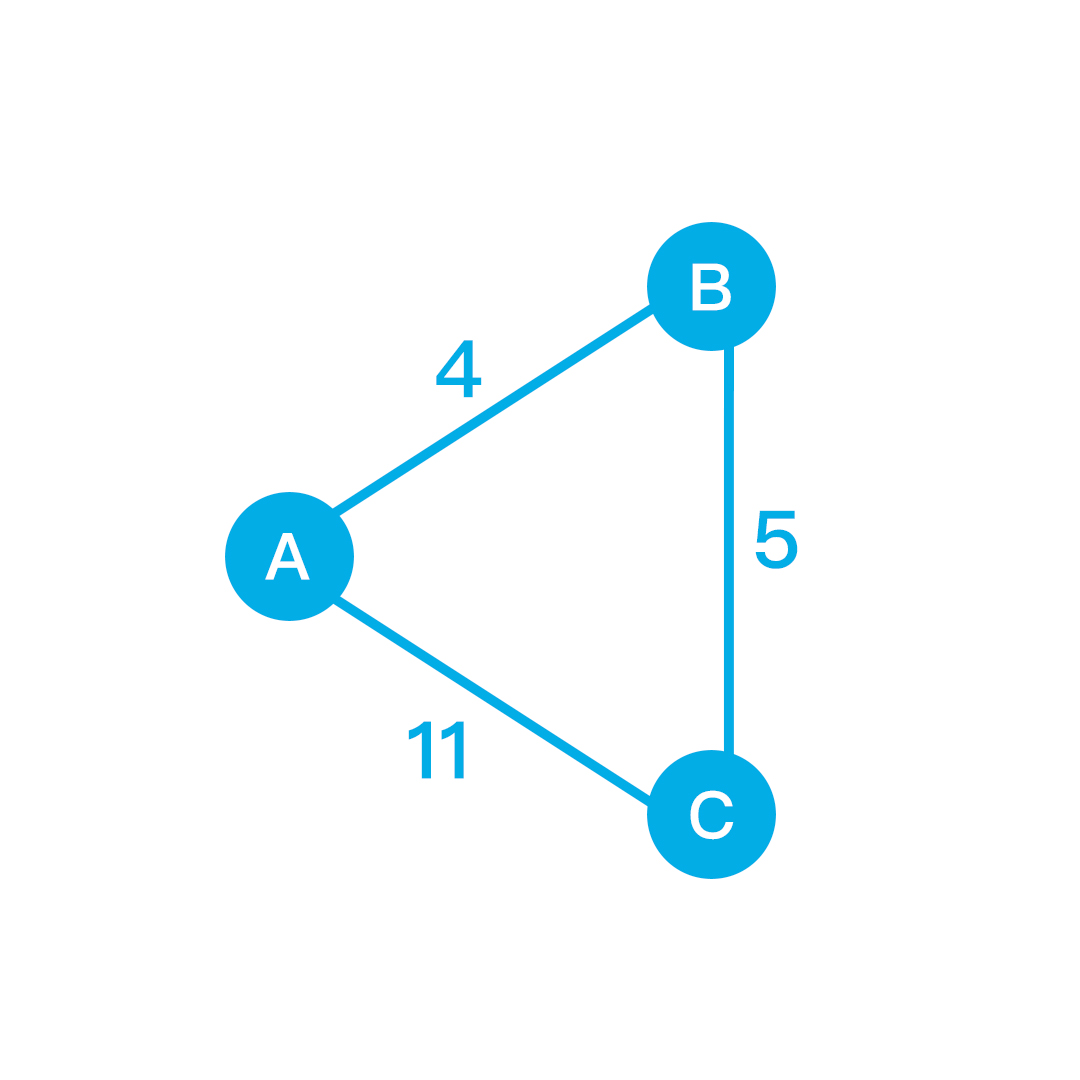
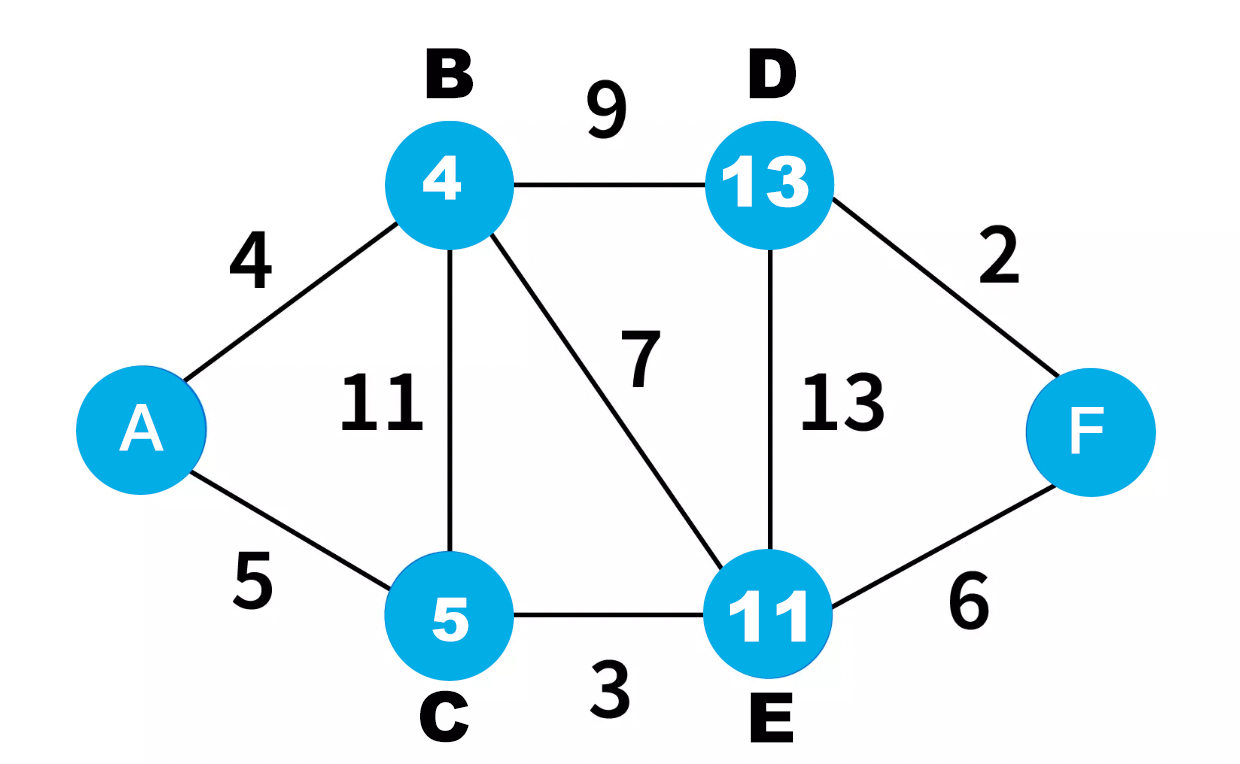
In the above example we have three nodes. And we will see use node A as source node. So from A to A distance is 0, and other node's distance is set to infinity. 

From A to B or to C, the shortest edge is 4. So we will go to B first and set the distance as shortest distance. From B we will reach out the neighboring nodes. We have only one node C. So here B is marked as visited. And the total edge distance is 4+5 which 9. So from A to C the distance is 9 if we go through B. C does not have any unvisited nodes.

Now once again from A, we can visit C and but we see that here the edge is 11 which is greater than 9. So the shorted distance would be 9 to C going through B. 

Algorithm

1. Mark the source node with a current distance of 0 and the rest with infinity.
2. Set the non-visited node with the smallest current distance as the current node, lets say C.
3. For each neighbor N of the current node C: add the current distance of C with the weight of the edge connecting C-N. If it is smaller than the current distance of N, set it as the new current distance of N.
4. Mark the current node C as visited.
5. Go to step 2 if there are any nodes are unvisited.

Let's see how it all work

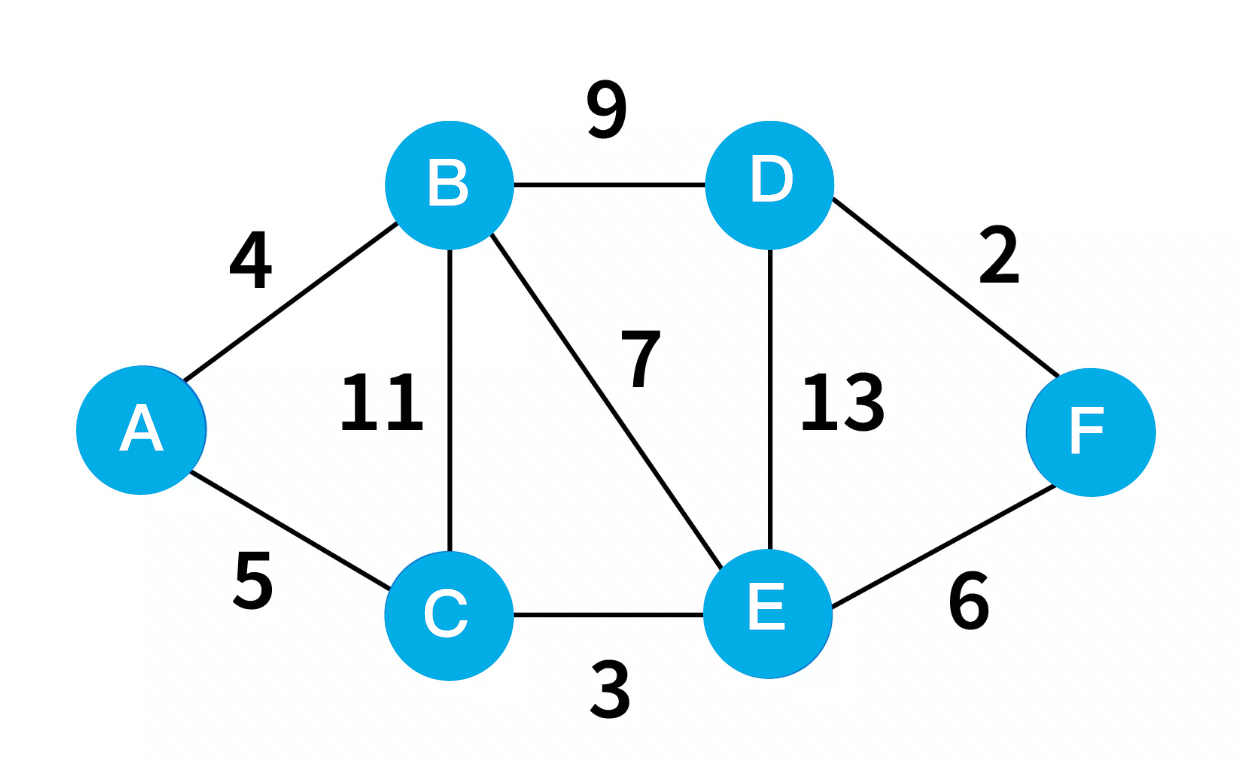
Lets assume the below graph as our input with the vertex A being the source.

1. Initially all the vertices are marked unvisited.
2. The path to A is 0 and for all the other vertices it is set to infinity.
3. Now the source vertex A is marked as visited.Then its neighbours are accessed(only accessed and not visited).
4. The path to B is updated to 4 using relaxation as the path to A is 0 and path from A to B is 4, so min((0+4),∞) is 4.
5. The path to C is updated to 5 using relaxation as the path to A is 0 and path from A to C is 5, so min((0+5),∞) is 5. Both the neighbours of A are relaxed so we move ahead. See the picture below
6. Updated value of node A and C are 4 and 5 respectively.
7. Then the next vertex with least path is picked and visited. So vertex B is visited and its unvisited neighbours are relaxed. After relaxing path to C remains 5, path to E becomes 11 and path to D becomes 13. See the picture below
8. Updated value of D and E is 13 and 11 respectively.
9. Then vertex C is visited and its unvisited neighbour E is relaxed. While relaxing E, we find that the path to E via C is smaller than its current path, so the path to E is updated to 8. All neighbours of C are now relaxed. See the picture below
10. The updated value of E is 8 now.
11. Vertex E is visited and its unvisited neighbours D and F are relaxed. As only vertex F is unvisited only, so F is relaxed. Path of B remains 4, path to D remains 13 and path to F becomes 14(8+6).
12. Then vertex D is visited and only F is relaxed. The path to vertex F remains 14.
13. Now only vertex F is remaining so it is visited but no relaxations are performed as all of its neighbours are already visited. See the picture below
14. As soon as all the vertices become visited the program stops.

Comment