In the sense of Dijkstra's or Bellman Ford's algorithm edge relaxation property is the core. Understanding edge relaxation plays vital role in understanding the shortest path algorithms along with graph theory.
d[v] = min{ d[v], d[u] + c(u, v) }
The above is the mathematical representation of the edge relaxation. We may simply break down with a pseudo code
if ( d[u] + c(u, v) < d[v] ) then
{
d[v] = d[u] + c(u, v)
}
Now, I know from the first glance, the mathematical model or the code do not make any sense. Let's dig deep into them.
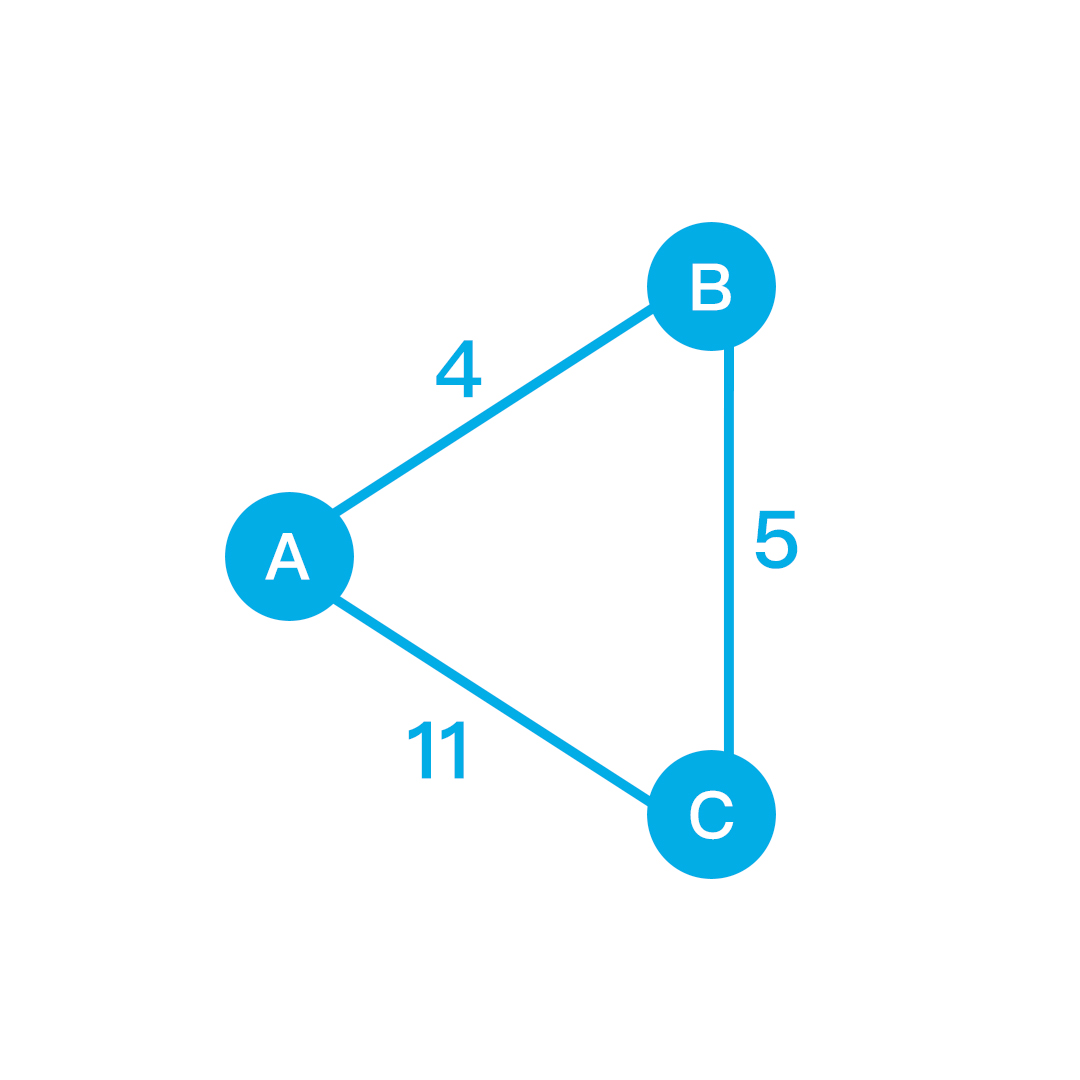
Here's the representation
Initially we also introduce an initial node and we name with s. You may also replace u, v based on your nodes' names.
The mathematical model or the pseudo code is used to find the minimum distance between two nodes.
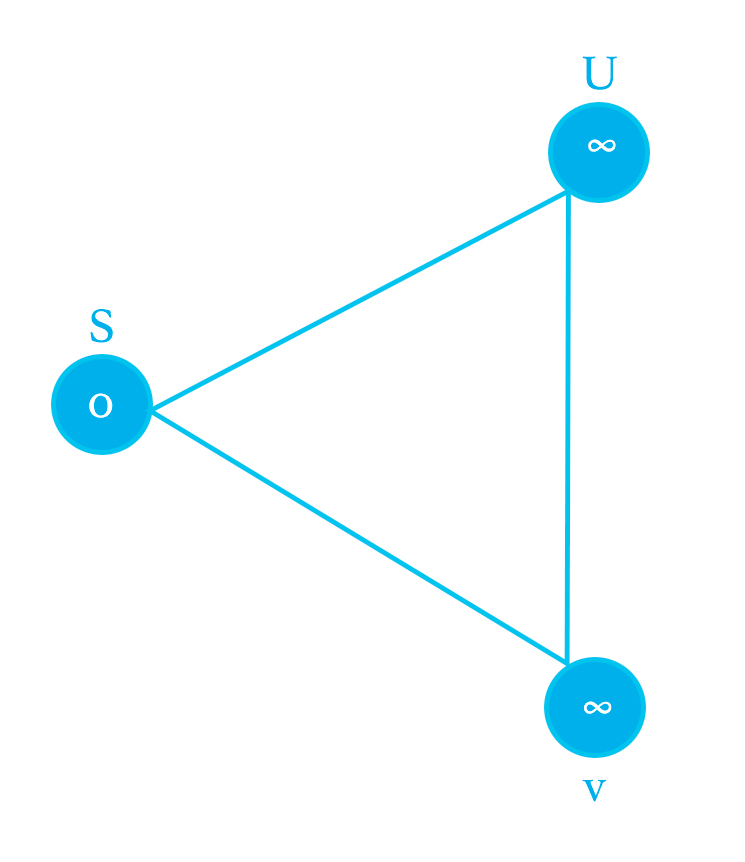
Here we will introduce the following based
Here S is the initial node or vertex and the distance to itself is 0, so d(s) is equals to 0. And then other nodes we set do infinity d(u) and d(v) to ∞.
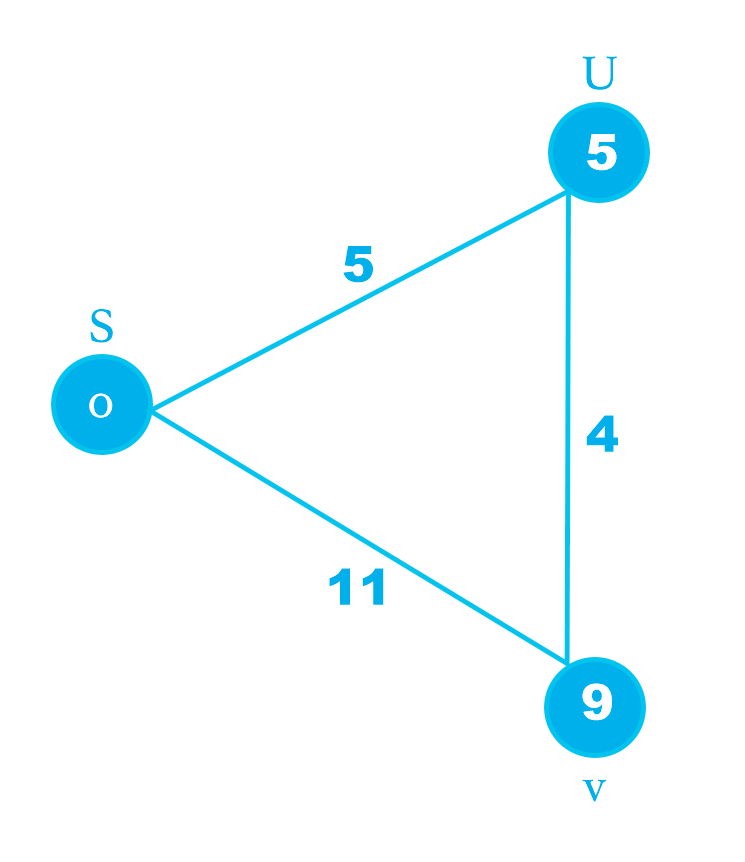
Now let's set up some random values for the edges.
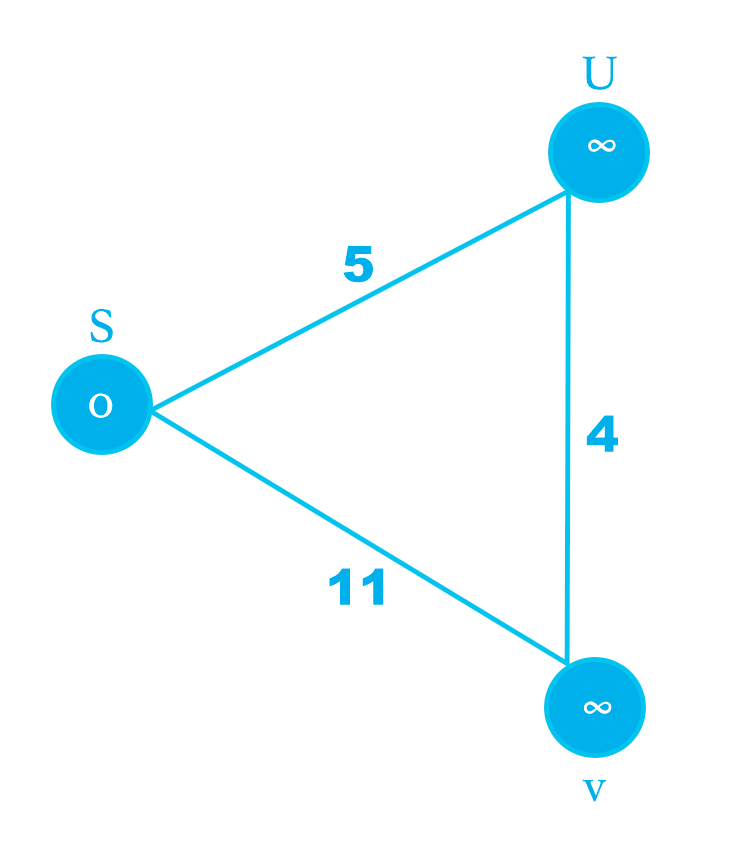
Here we have introduced some randoms values to the edges. So let's calculate the cost to reach to U from S. This is also called relaxing U node. We will use the mathematical formula for that.
Steps and value
So if use the mathematical formula
d[s] + c(s, u) < d[u]
0+5 < ∞
So if use pseudo code or the formula the value for d(u) is 5. And then for other two nodes we can find the values. Let's ee the current changes and nodes
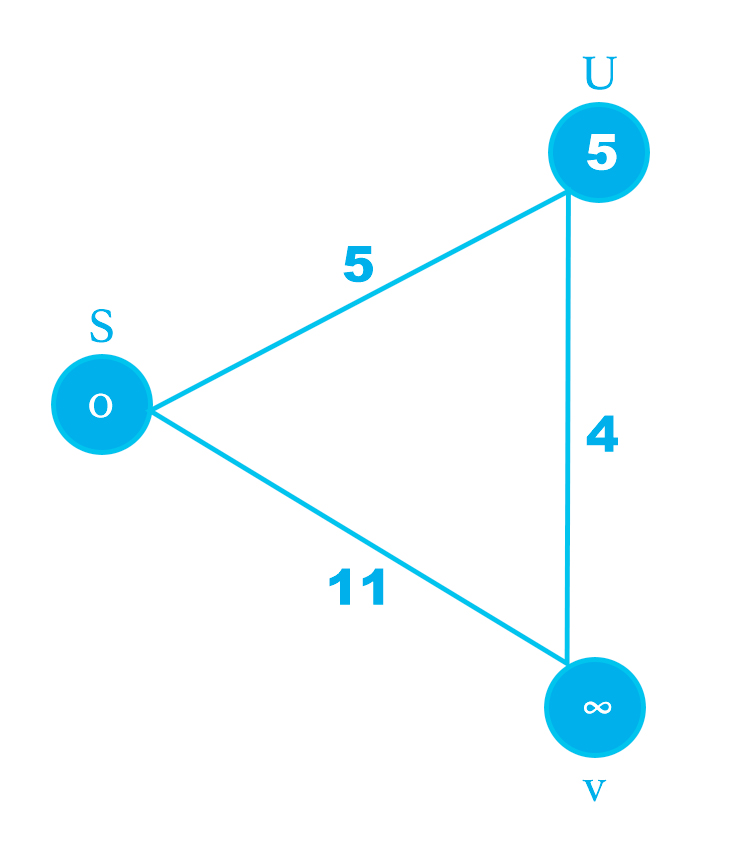
So currently d(u) is 5. Now we would be able to calculate d(v) from d(s). We will use the the same mathematical formula and this time we are relaxing node V.
Steps and value
d[u] + c(u, v) < d[v]
5+4 < ∞
Here d(u) is 5(already calculated) and c(u, v) is 4 which is the weight value. Now the value of d(v) is 9. So this from S to V through U node
Now we will go to V node from S node directly. Here we already see weight value is 11. Let's calculate using the formula
Steps and value
d[s] + c(s, v) < d[v]
0+11 < ∞
Now we have another d(v) value which is 11. Now this value directly from S to V. We also have earlier value of d(v) which is 9, this come from going through V node.
So finally we can say that we can use edge relaxation theory could solve dijkstra's algorithm.