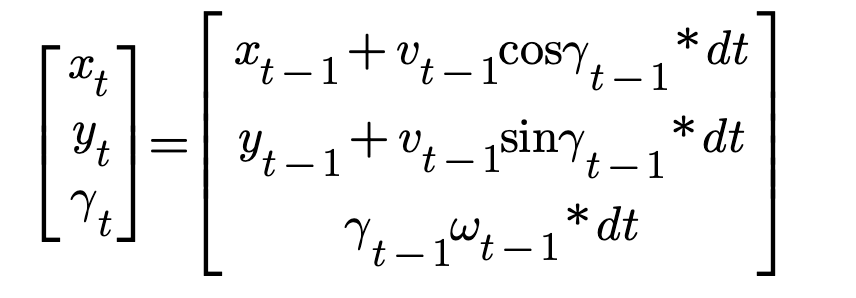Here we will focus how to make a state space for a mobile robot. Along the way, we will learn about differential mobile robot. A differential mobile robot is a robot whose wheels are driven indepdently. A state space model is represented by the below equation
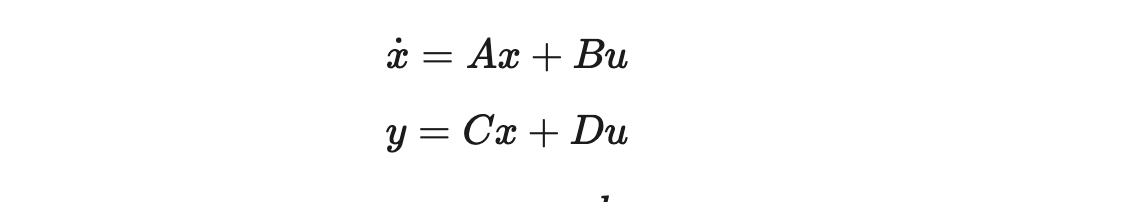
What is state space model?
If we use a state space model we would be able to predict the motion of a robot from one timestamp to another. The above equation would be very useful and we will come to it later and we will also derive the equation. State space model shows how the current position and orientation changes due to the impact of the input from the real world.
Position is represented by using x, y and z position.
Now let's assign angle associated with each axis and each angle is anti-clockwise. X coordinate rotates with alpha, Y coordiate rotates with beta and Z cooridinates rotates with gama angle.
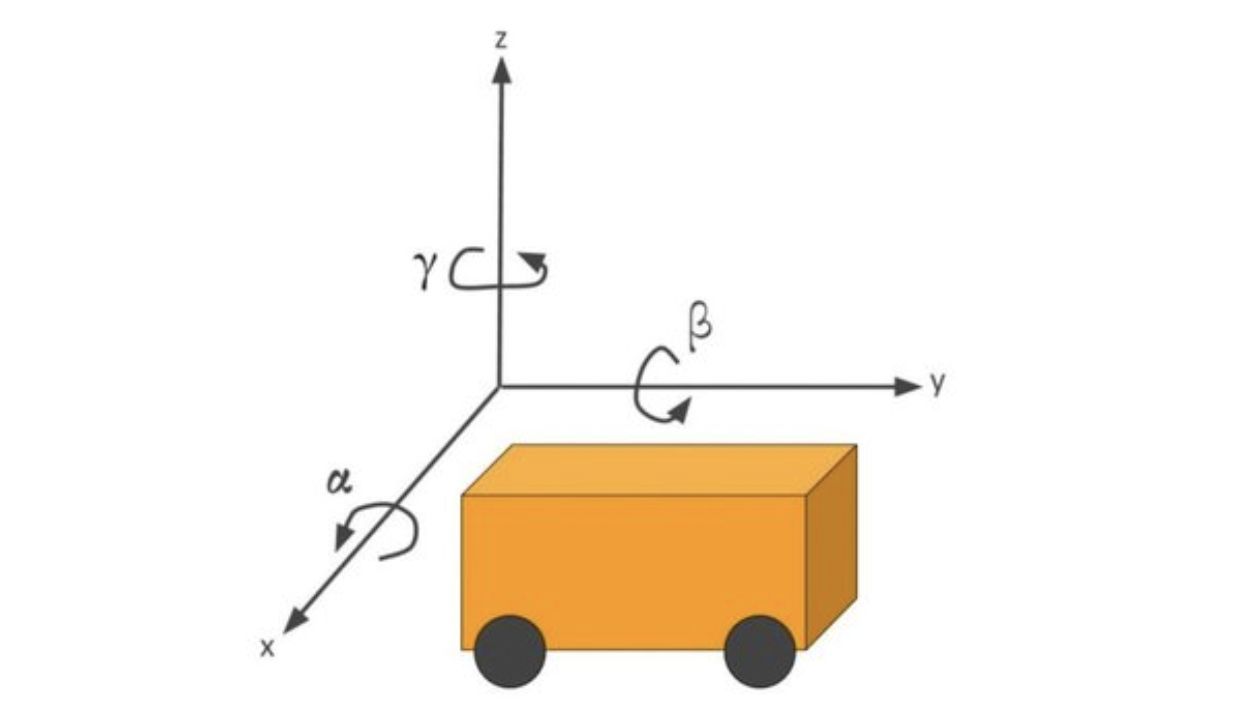
Let's create our Model
Let's for the sake of this tutorial we consider a very simple robot moving on x y flat. This means x y are our coordinate plane.
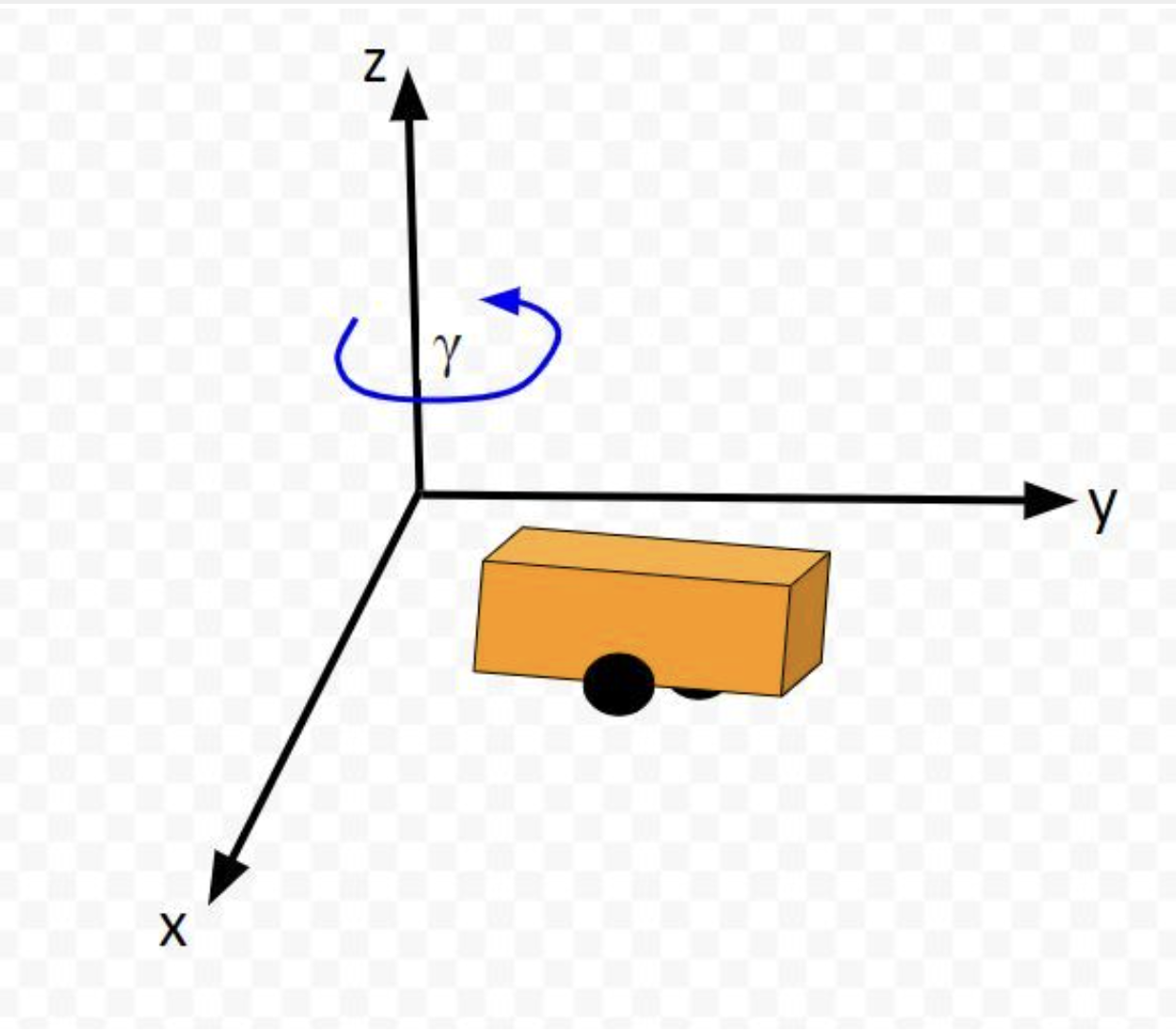
If the robot moves, it will have a movement on z coordinate too. So actually x y coordinate movement triggers z coordinate too. Let's take a top view or ariel view of the
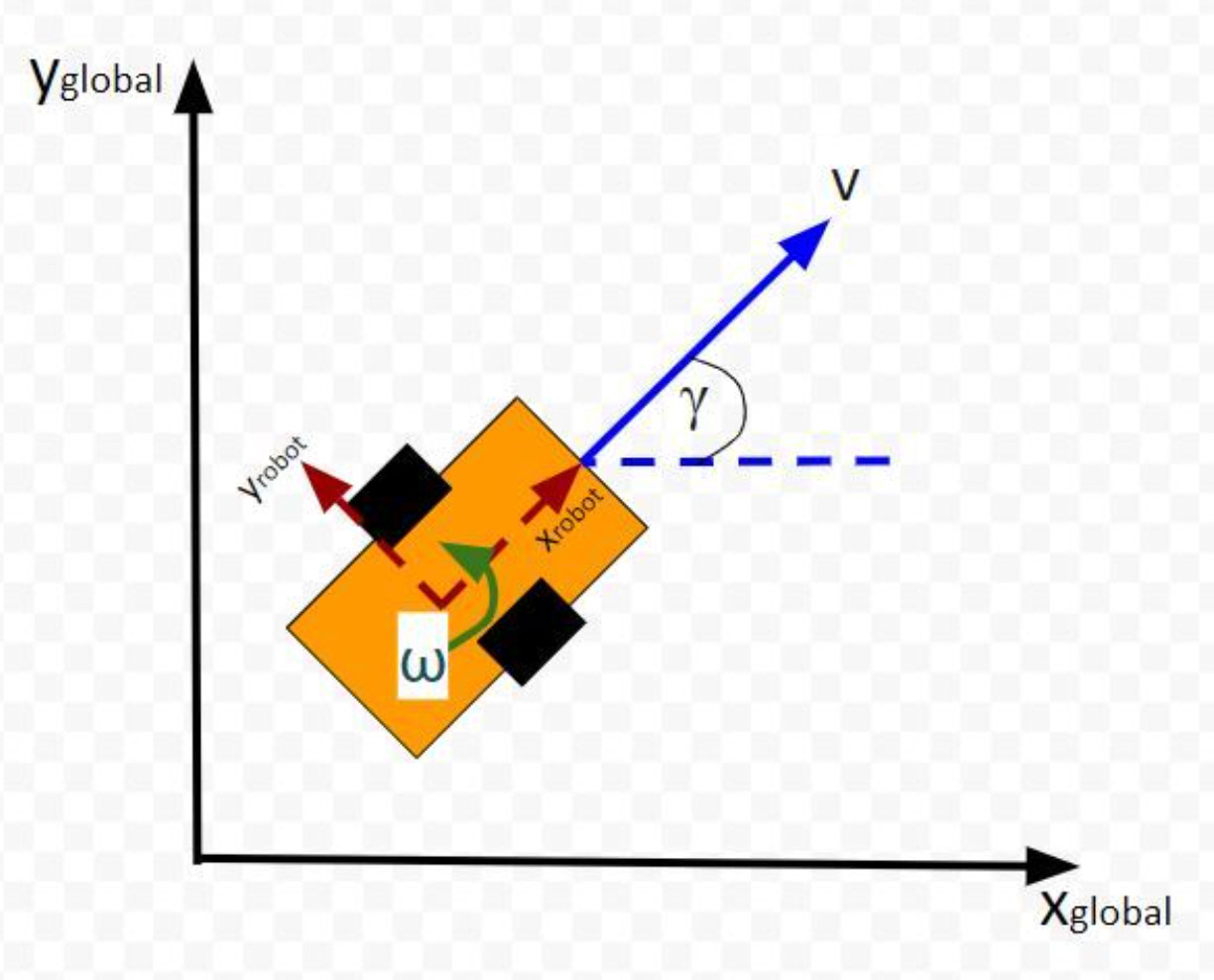
The z coordinate value is often associate with something called orientation. The x y position coordinate and z orientation together could be put in a mathematical form. This is called state vector. But for z coordinate we don't put z value directly, rather than we put rotation angle which is expressed using greek letter ϒ. This is called yaw angle.
More about state vector
A state vector is a mathematical representation of the system's current state. It is a set of variables that characterize the internal state of the system at a particular time. The state vector contains all the necessary information that allows us to predict the future behavior of the system. In this article, we will explore the basics of control systems and the significance of state vectors in control systems.
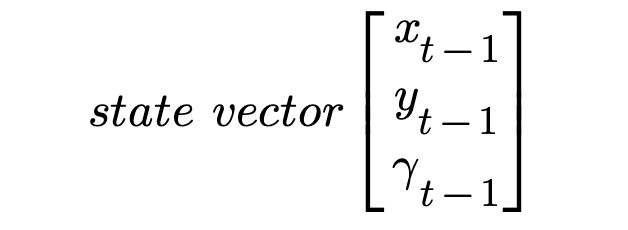
Our state vector in terms of time t-1. The last one is called yaw angle rotation around z axis. We can also xt-1 is the distance travelled by t-1 timestamp.
Next timestamp and distance
Now let's derive the next timestamp distance for the robot movement. We know distance = velocity * time. Applying this formula we can derive the state