Markov chain is a mathematical chain or model that describes state transition. It describes change or transition from one state to another state.
A state space could contain a variety of events or actions about a certain thing. A state space could be about the weather of a day. A day could be sunny, rainy or windy or another status.
A day could be sunny, then markov chain would tell us what's the likelyhood of a rainy day. Now, it would tell us this likelyhood totally based on the current state of sunny day. A day could have many states.
Now let's take a look at a simple example.
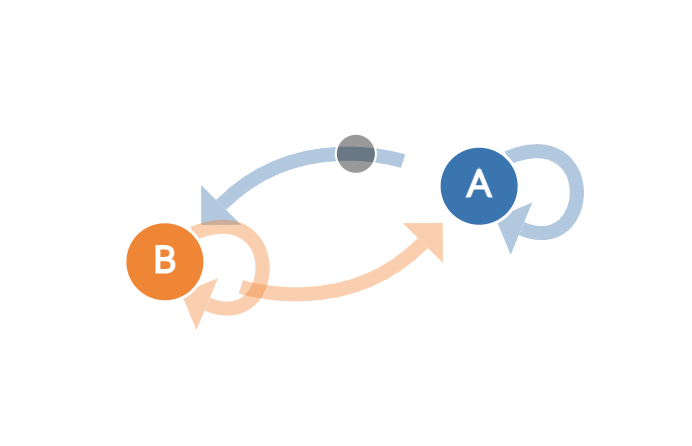
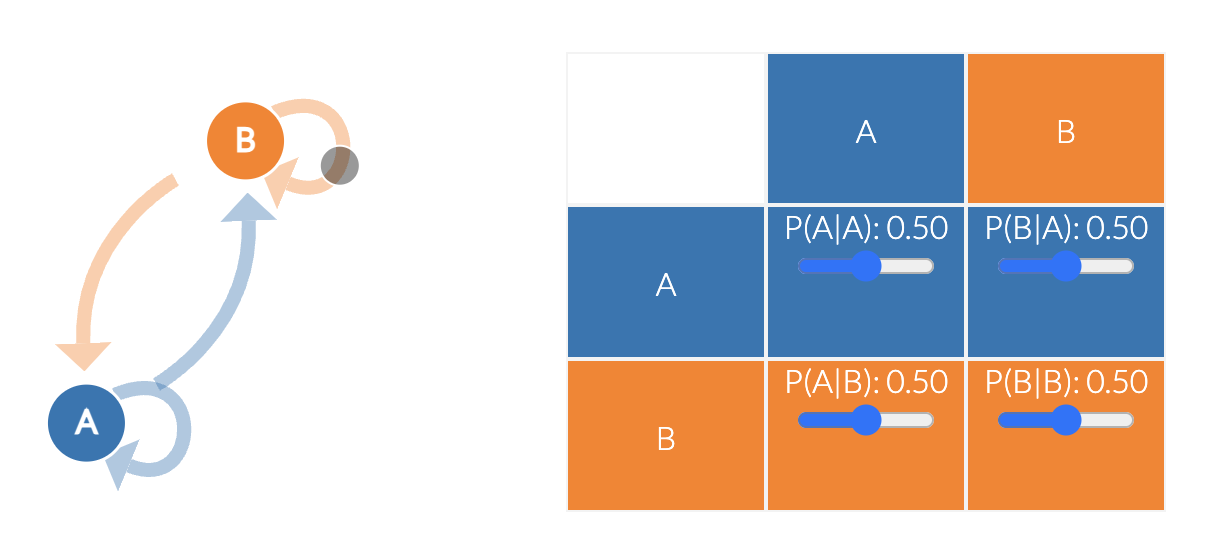
Here we have 2 states, but there are 4 possible transition. Look at the arrow that connects with each other. We see that transitions coule be
For 2 states, we have four transitions. If you have more states, then you will have more possible transitions. Now instead of drawing pictures, we may present in a matrix form with row and column. Within each cell of a matrix we mention the transition probability.